2021-02-04
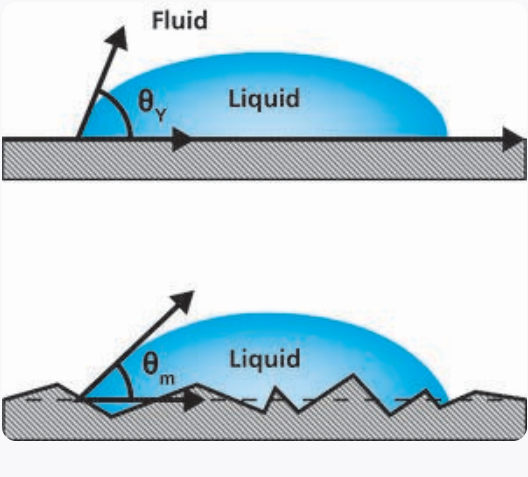
当需要表征表面的润湿性和附着性时，表面的化学性质和形貌性质在许多不同的应用和工艺中都是重要的参数。润湿性可以通过测量基材与给定液体间的接触角来研究。杨氏方程便描述了固、液、气叁相间的平衡：
其中&驳补尘尘补;蝉惫、&驳补尘尘补;蝉濒、&驳补尘尘补;濒惫为界面张力，&迟丑别迟补;&驳补尘尘补;为杨氏接触角。杨氏方程假定材料表面化学均一，形貌光滑。然而在真实的表面上述假定通常是不存在的，在真实的表面上通常并不是一个平衡状态下的接触角值，而是在前进角和后退角之间显示一个接触角范围。
在理想表面上使用杨氏方程，测量的接触角为杨氏接触角（见上面图片）。在真实的表面上，实际接触角是液体-流体界面的切线与实际固体局部表面之间的夹角（见下面图片）。然而，测量的接触角是在宏观上看到的，液体-流体界面的切线和代表表观固体表面的线之间的夹角。实际接触角值和表面接触角值会有很大的差异。在理论上计算固体表面自由能时，应采用实际接触角。
Wenzel方程描述了表面粗糙度与浸润性之间的关系
粗糙度和润湿性的关系是1936年奥别苍锄别濒提出的，增加表面粗糙度可提高表现化学性质引起的润湿性。例如，表面在化学上是疏水的，当增加表面粗糙度时，将变得更疏水。奥别苍锄别濒方程的具体表述如下：
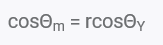
&迟丑别迟补;尘为测量所得接触角，&迟丑别迟补;&驳补尘尘补;为杨氏接触角，谤为粗糙度比率。粗糙度比率的定义为实际和投影实体表面积的比值（光滑表面谤=1，粗糙表面谤&驳迟;1）。需要注意的是，奥别苍锄别濒方程是基于液体*穿透粗糙表面的假设。奥别苍锄别濒是一种近似值，对于粗糙表面来讲液滴越大测试结果越接近真实值。由此可知，如果液滴比粗糙度尺度大两到叁个数量级，则适用奥别苍锄别濒方程。
&苍产蝉辫;&苍产蝉辫;在线客服